量子力学第二章

量子力学第二章

波函数

满足条件

1. 连续性
2. 单值性
3. 有限性

波函数的统计解释

波函数在空间中某一点的强度（振幅绝对值的平方）和在改点找到粒子的概率成正比。

数学表达式

$W(x,y,z)=C\int_\infty\Phi^*\Phi d\tau$

归一化

波函数在乘上一个常数后并不会改变在空间各点找到该点的几率，即不会改变该波函数下所描述的状态。

归一化条件

$\int_\infty\Phi^*\Phi d\tau=1$

态叠加原理

定义

如果一定情况下ψ1，ψ2是体系的可能状态，那么他们的线性叠加态ψ=c1ψ1+c2ψ2也是体系的可能状态。或者说当体系处于ψ1和ψ2的线性叠加态时，体系既处于ψ1也处于ψ2。

波函数动量描述与位置描述转化

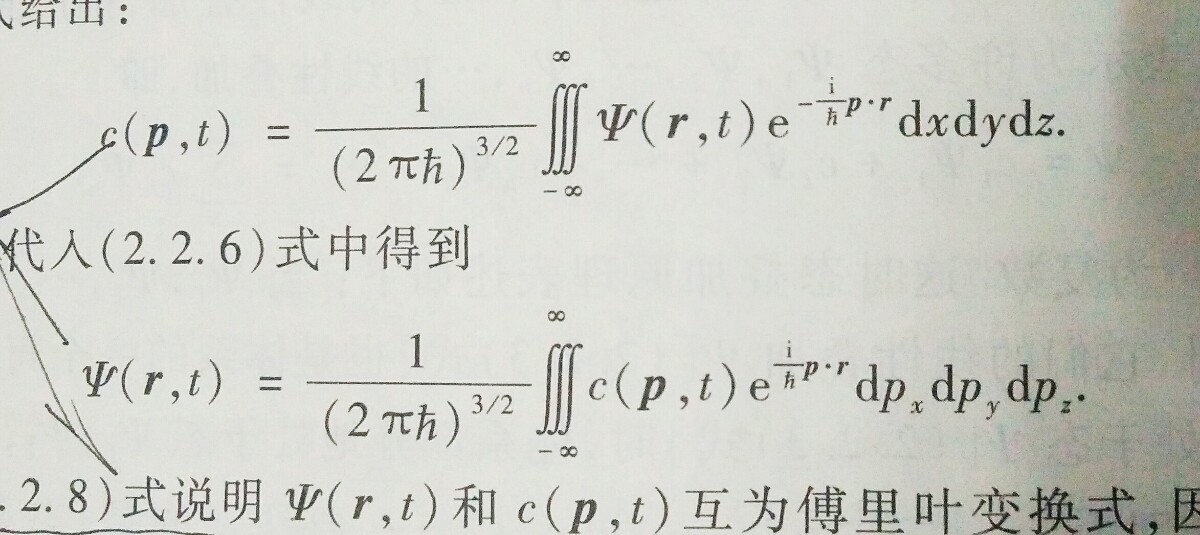
量子中的守恒

波函数归一后将保持归一状态而不随时间变化。

粒子流密度

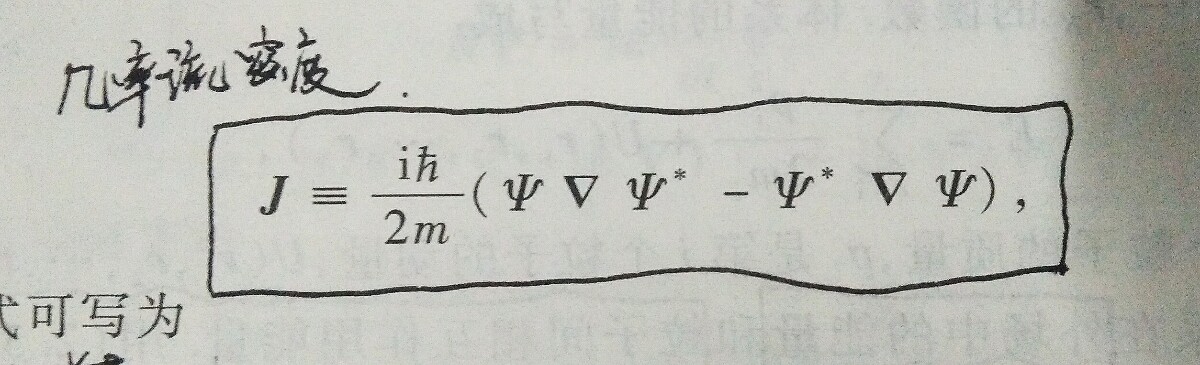
粒子数守恒

波函数求解

薛定谔方程

条件

1. 满足对含时间微商的微分方程
2. 方程是线性的
3. 方程系数应不包含状态参量

方程基本形式

$Hψ=(U+T)ψ$

H为哈密顿算符，U为势能，T为动能

一般解法

1. 列薛定谔方程
2. 求通解
3. 找边界条件带入求E
4. 归一化求波函数

定态薛定谔方程（能量本征方程）

是什么？

能量取得确定值时的方程。

数学表达式

$Eψ=(U+T)ψ$

有何性质

1. 几率，几率密度不随时间变化
2. 任何力学量的平均值不随时间变化
3. 任何力学量取各种可能值的概率分布也不随时间变化

怎么求解？

一维无限深势阱

一维空间运动的粒子其势能在一定区域内为0，而在此区域外势能无穷大的情况。

线性谐振子

在一维空间内运动的粒子势能为$1/2mω^2x^2$,ω为常量，则称这种体系为线性谐振子

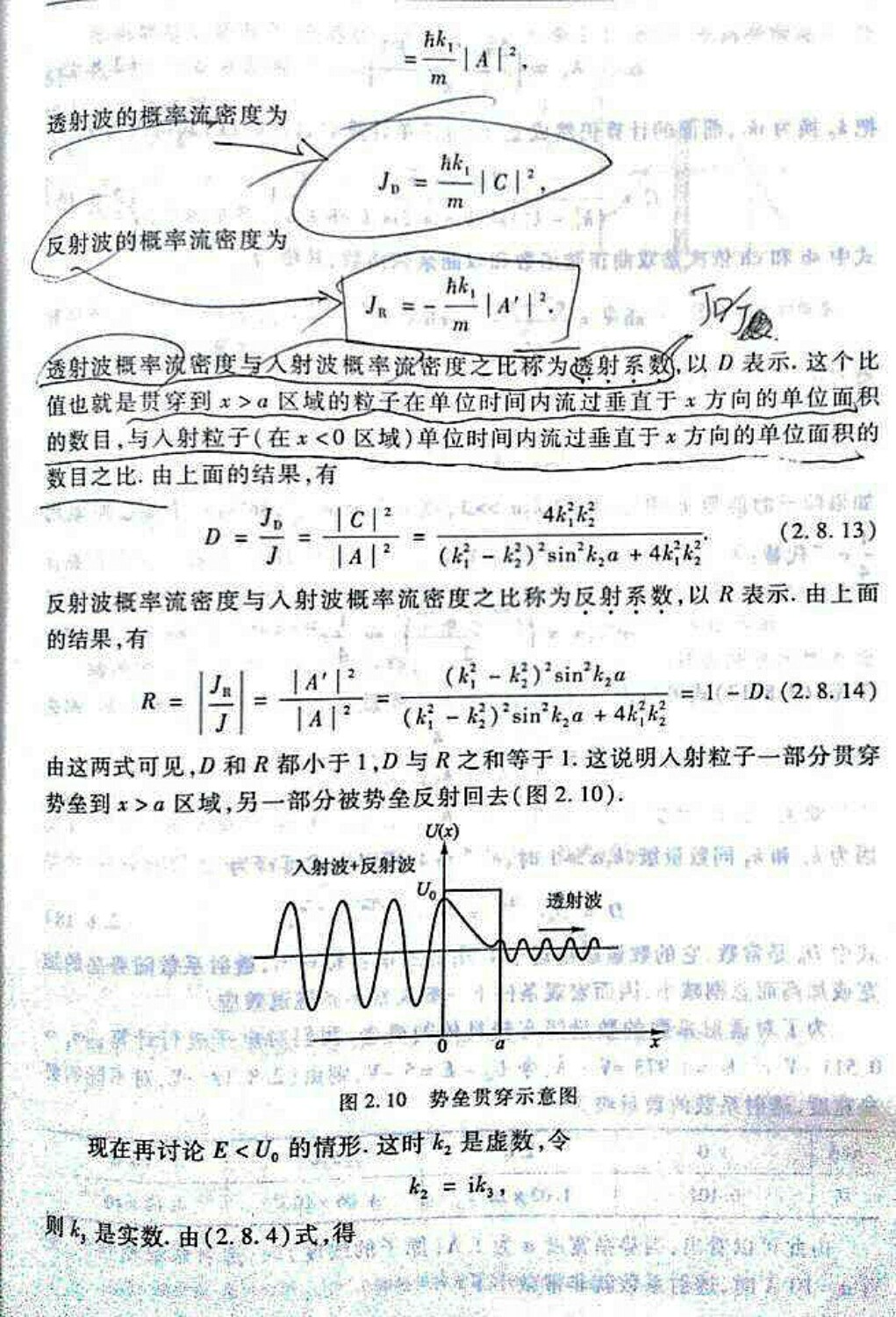
势垒贯穿（隧道效应）

粒子能量＜势垒高度时仍能贯穿势垒的现象